Infinity: A term referring to phenomena for which no end exists or can be conceived. Not to be confused with ►unboundedness.
It may have been the thought of immensely vast spaces or eons of time that first instilled in humans the idea of infinity. The Italian poet Giacomo Leopardi put it this way:
It was always dear to me, this solitary hill,
and this hedgerow here, that closes out my view,
from so much of the ultimate horizon.
But sitting here, and watching here, I thought,
I create interminable spaces,
greater than human silences, and deepest
quiet, where the heart barely fails to terrify.
When I hear the wind, blowing among these leaves,
I go on to compare that infinite silence
with this voice, and I remember the eternal
and the dead seasons, and the living present,
and its sound, so that in this immensity
my thoughts are drowned, and shipwreck seems sweet
to me in this sea.
(G. Leopardi, The Infinite, 1819)
At first infinity was ascribed simply to very long time intervals or distances, or to very large sets. The Greek word "eon" stands for an age, and in the plural ("eons") also for eternity. At that time, infinitude was not yet regarded as the opposite of finitude, but merely as an enlarged or prolonged version of finitude or as the sum of many finitudes.
Starting around 600 B.C., however, the Greek Presocratics began to study infinity more thoroughly.
The Greek Concept of Infinity
Anaximander (610 - 546 B.C.) introduced the concept of ►Apeiron, an infinite and infinitely divisible primordial form of matter that is the origin of all finite things: "Infinity is the origin of all things."
Pythagoras (570
- 497 B.C.) discovered the relations between the length of the sides of a rectangular triangle (a2 +
b2 = c2) and the ►irrational numbers as a solution to this equation.
Parmenides (515 - 450 B.C.) concluded that the totality of things is infinite as well. According to him, the universe has neither a spatial boundary (for what should be beyond such boundary?) nor a beginning in time (for what would have been the stuff out of which it evolved?) nor an end (for where should it go?) In this sense the world is spatially and temporally infinite.
Anaxagoras (500
- 428 B.C.) was the first to characterize infinity simply in terms of there being, in principle, no end to how large or small things are or can be: "For of the small there is no smallest, but always a smaller [...] But also of the large there is always a larger. "
Zenon of
Elea (490 - 430 B.C.) showed, by means of his paradoxes illustrating the delusive nature of motion (►Zeno's Paradox), that the infinite additivity of infinitely small parts, as well as the infinite divisibility of space, lead to contradictions with our experience and our natural judgments about the world.
Democritus (460
- 370 B.C.) concluded from Zeno's paradoxes that it is impossible to divide up bodies infinitely. There had to be a limit somewhere. The smallest components of all things are the indivisible ►atoms.
Plato(428 - 348
B.C.) characterized ideas as what make finite things the particular things they are, and as giving form to what would otherwise be an unordered and boundaryless world. Perfection is had only by these abstract forms, which "finitize" the constituents of the world encountered by the senses but which transcend that world and are not limited by it or its laws (and which therefore are infinite in that sense of the word).
Eudoxus (408 - 435 B.C.) was the first to postulate infinitely small numbers (anticipating the ►infinitesimal calculus) to determine lengths, surfaces, and volumes.
Aristotle (384 - 322
B.C.) solved Zeno's paradoxes by going back to Anaxagoras's thought that infinity is not actually realized anywhere. Rather, it exists only as potential infinity, that is, as the possibility of going beyond any particular finite number. Yet even the largest conceivable numbers and time intervals are still finite. Thus, there is no actual infinity in some kind of ready-made, completed form. Infinitude is not to be found in space or time, nor anywhere in nature. "In general, the infinite has this mode of existence: one thing is always being taken after another, and each thing that is taken is always finite, but always different."
Archimedes (287 - 212 B.C.) came up with a method of representing indefinitely large numbers to calculate the ►number of sand and also introduced limiting values to calculate the number ►Pi.
Aristotle's distinction between actual and potential infinity came to play an important part in the history and mathematics of infinity. After Aristotle there was at first a long intellectual standstill on the topic of infinity. That topic of was eventually taken up by theologians and theologically-minded philosophers, who brought with them a very different scale of values. While the Greek philosophers typically interpreted infinitude, unlimitedness, in terms of undifferentiatedness and regarded it as an imperfection, it was the finite that struck theologians as imperfect. Perfection lay precisely in the infinite nature of God (and only there).
Theological Infinity
Augustine (354 - 430)
denied that human beings area able to recognize the infinite on their own. Only ►God is able to do so due to His infinite nature, and only by striving to reach God can humans hope to come closer to infinity and find self-fulfillment: "Restless is our heart until it finds rest in Thou."
Anselm of
Canterbury (1033 - 1109) attempted to present a logical justification of faith by employing a concept of perfection in his definition of God: "A being than which nothing greater can be conceived."
Like Aristotle, Thomas Aquinas (1225 - 1274) denied the existence of actual infinity in material things while allowing for potential infinity: "Every kind of multitude must belong to a species of multitude. Now the species of multitude are to be reckoned by the species of numbers. But no species of numbers is infinite, for every number is multitude measured by one. Hence it is impossible that there can be an actually infinite multitude. " For Aquinas, only God can actually be infinite (making God the only perfect being).
Nicholas of Cusa (1401 - 1464) reintroduced the infinity of the world. Since nature was formed according to Divine imagination, God must have passed on His own infinity to the world as well. The universe therefore possesses at least some kind of copy of infinity. All opposites are united in infinity, since maximum and minimum coincide in the infinite and a circle can no longer be distinguished from a line.
Enlightenment Infinity
Giordano Bruno (1548 - 1600) described the universe not as potentially but as actually infinite and eternal, with the Earth occupying only a negligible spot within a gigantic space. Anything short of such a universe would be unworthy of the creative power of an infinitely powerful God. "I believe in an infinite universe, the effect of an infinite divine potency, because it has seemed to me unworthy of the divine goodness and power to create a finite world, when able to produce beside it another and others infinite: so that I have declared that there are endless particular worlds similar to this of the Earth. " Bruno paid with his life for this view.
Blaise Pascal (1632 - 1662) saw humanity as lost between the infinitely large and the infinitely small in nature: "For after all what is man in nature? A nothing in relation to infinity, all in relation to nothing, a central point between nothing and all and infinitely far from understanding either. The ends of things are impregnably concealed from him in an impenetrable secret. He is equally incapable of seeing the nothingness out of which he was drawn and the infinite in which he is engulfed. "
Baruch de Spinoza (1632 - 1677) returned to the ancient notion of the Apeiron by replacing the personal God of traditional theism with a conception of God as an all-pervading substance that is the basis of all appearances in nature. This substance is spatially and temporally infinite and thus the cause not only of all things but also of itself.
René Descartes (1596 - 1650) did not believe in the actually infinite, but he did believe in indefiniteness: "In every case where we can find no limit to some aspect of a thing, we shall not assert that it is infinite, but we shall regard it as indefinite. For example, we cannot imagine an extension so large that we cannot understand the possibility of an even larger one. So we shall say that the size of possible things is indefinite. Again, a body cannot be divided into so many parts that we cannot understand that each of these parts is divisible still further. So we shall make it our opinion that quantity is indefinitely divisible. Again, we cannot imagine that the number of stars is so great that we could not believe that God would have been able to create still more. "
John Locke (1632
- 1704) granted that empty space, which does not have any boundaries to prevent the addition of ever further lengths, is infinite. However, he distinguished between space, on one hand, and the universe, on the other, holding that the latter — the totality of all material things — is of merely finite extension and is located within infinite space. The infinity of space, time, and numbers thus is merely potential. "It would be hard, I think, to find anyone so absurd as to say he has the positive idea of an actual infinite number."
Gottfried Leibniz (1646 - 1716) saw the world as being composed of infinitely many indivisible ►monads but rejected the idea of an infinite totality (whole) of things. "It is perfectly correct to say that there is an infinity of things, i.e. there are always more of them than can be assigned. But it is easy to demonstrate that there is no infinite number, nor any infinite line or other infinite quantity, if these are taken to be genuine wholes. The true infinite, strictly speaking, is only the absolute, which precedes all composition and is not formed by the addition of parts."
Despite his lip service rejection of actual infinity, Leibniz was one of the major figures involved in the mathematical revolution of the 17th century. While mathematics had previously only attempted to describe nature, it now began to deal with abstract objects that did not match anything in nature — objects such as the infinitesimal numbers, which are infinitely small numbers. Paradoxically, this abstract form of mathematics was able to describe the behavior of nature much better than its predecessors. Isaac Newton made use of infinite divisions of mathematical curves in his ►fluxion calculus, defying both Aristotle and the objections of contemporary philosophers and theologians. His efforts were rewarded by his discovery of ►laws of nature concerning gravity and the motions of solid bodies as well as a precise theoretical model of the solar system.
The Schism of Infinity
Since the time of Newton and Leibniz, infinity has had to tolerate quite diverse treatments in the sciences, mathematics, and philosophy. Mathematicians and natural scientists began to include in their calculations first the infinitely small and then the infinitely large. Consequently, after the 17th century mathematical theories of infinity split off onto a separate route of development, while philosophers and theologians continued theorizing in largely the same way as before:
George Berkeley (1685 - 1753) regarded nature as consisting only of perceptions and thus only of finite things. Only perceptions are real manifestations of God's spirit, outside of which there is nothing in nature. Thus the world exists only insofar as it is perceived either by God our by us. Concepts referring to things that cannot be perceived by the senses, such as 'infinity', have no place in philosophy: "Whether the object of geometry be not the proportions of assignable extensions? And whether there be any need of considering quantities either infinitely great or infinitely small? [...] And whether it be not unnecessary, as well as absurd, to suppose that finite extension is infinitely divisible?"
Immanuel Kant (1724 - 1804), by contrast, distinguished between perceivable phenomena and the things as they are in themselves, the latter of which are beyond our cognition. "Without sensibility no object would be given to us." Space and time are merely forms of our intuition and necessary for us to impose any congitive order on the phenomena in the world. Consequently, infinity does not exist independently of us either, since it cannot be perceived. Infinity is merely "a principle for the enlargement and extension of experience as far as is possible for human faculties. It forbids us to consider any empirical limits as absolute. It is, hence, a principle of reason ... ".
Georg Hegel (1770 - 1831)
regarded the finite and the infinite as a dialectical unit. The infinite realizes itself only within the finite. But the infinite is not just the negation of the finite; rather, actual, "genuine" infinity is the negation of potential or "bad" infinity.
Potential infinity is like "the straight line, at the two limits of which alone the infinite is". True infinity, by contrast, is like a circle, "a line which has reached itself, which is closed and entirely present, without beginning and end."
Ludwig
Feuerbach (1804 - 1872)
saw human beings in a schism between the next world and this world, between the infinitude of God and the finitude of their own nature. The consciousness of infinity, however, is nothing but a consciousness of the infinity of one's own consciousness. The knowledge of God is humans' self-knowledge and eventually leads to their liberation from God. This liberation will transform "theologians into anthropologists, lovers of God into lovers of man, candidates for the next world into students of this world." For only ►atheism, the recognition of the origin of infinity in one's own human consciousness, "gives back to nature and humankind the dignity of which theism has despoiled them."
Mathematical Infinity
As has already been mentioned, concepts of infinity in mathematics did not differ noticeably from those in philosophy up to the 17th century. Here, too, infinity was at first accepted only as an approximation, that is, only as potential infinity. The expression
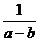
approaches infinity if the values a and b approximate each other. However, when a and b are equal, the expression becomes meaningless. Mathematics does not permit division by 0.
This resistance to actual infinity first began to crumble in the 17th century with Newton's and Leibniz's ►infinitesimal calculus, the mathematics of infinitely small numbers. Still, although the infinitesimal calculus was obviously successful and accurately described processes in nature (such as planetary motions, for example), in the eyes of many contemporaries actual infinity remained a suspicious, if not specious, notion.
S.F.
Lacroix (1765 - 1843), the author of the standard textbook on infinitesimal calculus in the 18th century, wasted no time in rejecting infinity, writing in the book's introduction, "Infinity as the last element of quantity, is itself an exclusive limit, a limit that quantities can never reach. The associated concept is but a negative concept, for each quantity that I imagine as real and use in my calculus is, for that very reason, not infinite. " As late as 1831, Carl Friedrich
Gauss (1777 - 1855) complained: " I protest against the use of infinite magnitude as something completed, which is never permissible in mathematics. Infinity is merely a way of speaking, the true meaning being a limit which certain ratios approach indefinitely closely." This, however, did not prevent Gauss from developing fundamental methods of differential geometry, which is based on ►infinitesimal calculus and operates with infinitely small numbers. Bernard Bolzano (1781 - 1841)
was the first mathematician to systematically rebel against the anathematizing of infinity. The world, he thought, is full of actual infinites, so that it does not make any sense to exclude them from mathematics. The set of all points in a line is infinite. Every time interval contains infinitely many moments. The number of digits after the decimal point of the square root of 2 is infinite. And the human spirit, according to Bolzano, is capable of imagining an infinity as a whole, for to do so you do not need to imagine every single component of this infinite whole in isolation. Bolzano succeeded in developing his own mathematics, one that enables us to calculate infinite quantities without inconsistency. He also proved that the number of points in a region of the ►number ray does not depend on its length. His results were published posthumously under the title Paradoxes of Infinity.
150 years after its introduction into mathematics, Karl Weierstrass (1815 - 1897) provided a logical foundation for the ►infinitesimal calculus by deriving the use of infinitely small numbers from limiting values.
► Bernhard Riemann (1826 - 1866) was the first to prove that a finite surface has the same number of points as an infinite one by projecting the points in the surface of a sphere onto a plane.
Richard Dedekind (1831 - 1916)
developed the first mathematical definition of an infinite set. According to Dedekind, a set is infinite if it contains the same number of elements as one of its proper subsets. Conversely, a set is finite if it contains more elements than each of its proper subsets. Last but far from least, ►Georg Cantor (1845
- 1918) fully rehabilitated the actuality of infinity in mathematics. Against the resistance of conservative mathematicians, he single-handedly developed ►set theory and the mathematics of ►transfinite, that is, actually infinite numbers. It is not by accident that in the mathematics sections of this dictionary almost every other concept relates to Cantor either directly or indirectly. The mathematician ►David Hilbert summarized Cantor's achievements as follows: "No one shall drive us from the paradise that Cantor created for us."
► Ernst Zermelo (1871 - 1953) and Abraham Fraenkel together formulated a consistent axiomatic system for Cantor's ►set theory. It contains nine axioms* and constitutes the foundation for almost all branches of mathematics, much like ►Euclid's axiomatic system of geometry.
► Bertrand Russell (1872 - 1970) discovered ►Russell's paradox, thereby indirectly proving that there is no largest possible infinity.
► Luitzen Brouwer (1881 - 1966) demonstrated that it is impossible to prove geometrically that the sets of points of planes with different dimensions have the same cardinality. Proving this arithmetically (see ►Dimension), on the other hand, is pretty simple and had already been done much earlier by Cantor.
► Kurt Gödel (1906 - 1978) proved the incompleteness of all axiomatic theories in 1931; seven years later he proved that the ►continuum hypothesis is not refutable within Zermelo's axiomatic set theory.
► Paul Cohen 1934 - 2007) proved in 1963 that the opposite of the continuum hypothesis is not refutable either. With that, the continuum hypothesis had been established as one of the undecidable sentences of axiomatic mathematics.
* The nine axioms of Zermelo's and Fraenkel's set theory are as follows:
I. Axiom of Extensionality: If every element of a set X is also an element of Y and vice versa, then X = Y.
II. Axiom of Subsets: If x is any object in the domain then there is a set {x} containing x and only x as element.If a, y are any two objects in the domain then there is always a set {x,y} containing both x and y but no element distinct from x or y.
III. Axiom of Specification: If Z is a set, and P is any property that may characterize all elements x of Z, then there is a subset Y of Z containing all and only those x in Z that satisfy the property P.
IV. Axiom of Powersets: For each set X there is another set PX containing all and only the subsets of X
V. Axiom of Union: For any set X there is a set Y containing all and only those sets that are members of some member of X.
VI. Axiom of Choice: If X is a set all of whose elements are distinct from 0 and pairwise disjoint, then their union Sx contains at least one subset that has one and only one element in common with each element of X.
VII. Axiom of Infinity: There is at least one set Z that contains the empty set as element and is such that for each of its elements x there is another element of the form {x}.
VIII. Axiom of Replacement: If we replace the elements x of a set X definitely with any elements x' of the domain then this domain will contain a set X' that contains all these x' as elements.
IX. Axiom of Foundation: Every non-empty set X contains a member y such that X and Y are disjoint sets.