Parallels (from Greek para, "next to", and allelon, "one another"): Lines that run in the same direction and intersect only at an infinite distance.
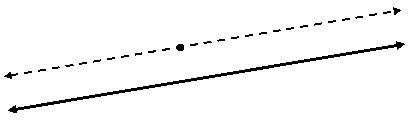
Euclidian Geometry: Exactly one parallel per line and point.
In Euclidian geometry there is for each line exactly one parallel line through any given point outside it. Euclidian geometry describes the properties of certain kinds of spaces, including, presumably, the three spatial dimensions of our ►universe. This is evidenced by the regularity in the distribution of cosmic ►background radiation. In Euclidian spaces the sum of the angles of a triangle is exactly 180 degrees. It can be shown that the parallel axiom and the 180-degree angle sum are mutually contingent upon each other and hence equivalent. There are also non-Euclidian spaces:
There are no parallels whatsoever on the surface of a sphere or an ellipsoid, because here all straight lines —
the great circles — already intersect at finite intervals. The sum of the angles of a triangle here depends on its dimensions and exceeds 180 degrees.
On a saddle or toroidal surface, there are infinitely many parallels for each line and each point outside it. In addition, here the sum of the angles of a triangle once again depends on its dimensions; this time, however, that sum is smaller than 180 degrees.
The statement that parallels intersect in the infinite is not equivalent to the statement that they don't intersect at all. This is because the foundations (or axioms) of Euclidian geometry can be formulated much more simply if we introduce a point of intersection in infinity. This infinite point of intersection is not merely theoretical; it is real and sometimes even visible, as in ►perspective, or in poetry (The Two Parallels by Christian Morgenstern):
Once went two parallels
out in the infinite,
two straight souls
and from a solid home.
They did not want to intersect
until their peaceful grave
this was, what to say,
both's secret pride and way.
But after ten lightyears
of such common traveling,
the lonesome couple felt
not really earthly anymore.
Were they still parallels?
They couldn't say, -
they were only like two souls flowing
together through eternal Light.
The eternal Light permeated them,
thus they became one in Him;
eternity swallowed them,
just like two seraphim.