Continuum hypothesis: A hypothesis by the mathematician Georg Cantor that there is no set whose cardinality is strictly between that of the ►Real Numbers and that of the Natural Numbers, which have minimal cardinality. As an equation, the continuum hypothesis can be formulated thus:
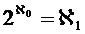
You may read up in more detail about this equation and the strange symbols it contains in the article on ►Cardinal numbers.
As►Cantor's biography has shown us, his proof of the continuum hypothesis dramatically failed, and he paid a high price for it. Nonetheless, in the early 20th century the continuum hypothesis became one of the most famous unsolved problems in mathematics. Many mathematicians tackled it — until 1930.
That was the year in which logician Kurt Gödel published his incompleteness theorem.* According to the theorem, every sufficiently consistent system of statements is incomplete. This means that in such a system there are always statements that cannot be demonstrated or refuted by means of the system itself. This is analogous to the proof discussed in the article on ►truth that there can't be a universal truth machine. The incompleteness theorem applies to mathematics and also, of course, to set theory.
All Mathematics is Incomplete
Gödel proved this theorem in the abstract, without providing any specific example of a statement that is in principle unprovable from within its system. This suggested an investigation of hitherto unsolved problems in mathematics in order to see whether one of them happens to involve just such a statement. Gödel undertook this investigation; his first suspect was the continuum hypothesis.
In 1937 he provided a proof that the continuum hypothesis cannot be refuted within set theory and that, therefore, it is consistent with all statements of set theory. This does not mean, however, that it is proven to be true. To prove this we would have to prove that its contrary is inconsistent with the statements of set theory.
Gödel did not succeed in getting any further with regard to this question. It was only in 1963 that Paul Cohen was able to prove that the contrary of the continuum hypothesis is also consistent with set theory. This finally established that the continuum hypothesis is undecidable in the system of classical logic — that is, it is neither true nor false. At the same time, it is one of the first concrete illustrations of Gödel's incompleteness theorem. Thus, it turned out that Cantor had never had a chance with any of his attempts at a proof during the 19th century.
The Third Level of Infinity
In the meantime, mathematicians have been considering whether to render the continuum hypothesis decidable by means of a meaningful expansion of set theory. However, they have dropped the idea of including Cantor's original version of the hypothesis. Like many mathematicians, Cohen thinks that the set of real numbers is so large that it could not possess the second smallest infinite cardinality. Therefore, the cardinality of the continuum would need to be larger than א1 in order to be part of an appropriate, usable system of set theory. Thus, in further developments of set theory the general tendency is now toward adopting the statement
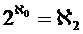
which, of course, raises the question what set would then correspond to the second level of infinity, namely to the cardinality of א1.
* The version of the proof that is probably easiest to understand for non-mathematicians can be found in Gödel, Escher, Bach by Douglas Hofstadter (see Suggested Readings).