dictionary.of-the-infinite.com

Practically all primitive peoples were familiar with numbers, though at first they were used only as a means to express quantities or volumes of objects: two apples, three pears, and so on. Isolating the numbers two and three from the apples and pears and treating them as objects in their own right requires abstraction, patience, leisure, and a certain distance from the things of everyday life. Professional priests and magicians were presumably the first who used numbers in isolation from things.

Initially only a limited amount of numbers were recognized: one, two, three, infinity. More numbers were added in the course of time, but infinity remained the largest number. The Greeks, who were already able to count as far as to 100,000,000, were the first to realize that infinity is not an object but a concept. This view conforms to contemporary mathematics, which does not recognize infinity as a number object — not even in the sense of the result of dividing by zero — but as a property of a ►set.

Before the invention of ►numbering systems it was difficult to write down very small or very large numbers. To save paper and for reasons of clarity we now use powers of ten: for example, 10¹² (pronounced "ten to the power of twelve") corresponds to 1,000,000,000,000, that is, to a 1 with 12 zeros. 10^-9 corresponds to 0.000000001. Some numbers are so large that they cannot be reasonably represented even as powers of ten. These numbers are represented instead as double powers of ten. In the article on ►parallel worlds, for example, you encounter the number 10 to the power of 10⁸⁰, that is, a 1 with 10⁸⁰ zeros.* To be better able to pronounce large numerical amounts we use Greek prefixes or number words. However, the fact that numerical words — like so many other things — are clearly larger in the ►USA than in the rest of the world adds to the confusion (especially when reading internet articles):

Number	Number word in English	US American	Prefix	Example
10³	Thousand	Thousand	Kilo (kg)	1 kg = 1000 g
10⁶	Million	Million	Mega (M)	1 megawatt = 1 million watts
10⁹	Thousand Million	Billion	Giga (G)	1 gigahertz = 10⁹ hertz
10¹²	Billion	Trillion	Tera (T)	1 teraflops = 10¹² flops**
10¹⁵	Thousand Billion	Quadrillion	Peta (P)
10¹⁸	Trillion	Quintillion	Exa (E)

More gigantic prefixes, such as Zeta (Z) = 10²¹ or Yota (Y) = 10²⁴, are used rarely, and then only by number fanatics in certain online dictionaries.

Apart from their sometimes enormous sizes, numbers at first glance look like simple structures. Their potentially complex and even astonishing properties were discovered only gradually. Even contemporary mathematics is still far from knowing all the properties of numbers. Thinking of numbers, the first thing that comes to mind is that they can be classified into various types:

Natural numbers are all positive numbers without digits after the decimal point, that is, numbers such as 1, 2, 3, 4, ... There is a ►countably infinite amount of natural numbers.

Integers are all numbers without digits after the decimal point, that is, -2, -1, 0, 1, 2, 3... The set of integers is also countably infinite.

Rational numbers (from Latin ratio, "calculation") are all fractions, that is, the results of a division such as 1/1, 1/2, 2/3, 1/4, and so on. These are numbers with either a finite number of digits after the decimal point (such as 1/4 = 0.25) or a periodic, that is, infinitely repetitive series of digits after the decimal point (such as 1/11 = 0.09090909).*** The rational numbers are also countably infinite.

All the remaining numbers are irrational numbers. These are numbers that are not fractions and hence have a non-repetitive infinite series of digits after the decimal point. Examples are the square root of 2 (1.41421356...)† and the number ►Pi (3.1415926...). Rational and irrational numbers together form the set of real numbers, also known as the "continuum". The continuum is not ►countable. Thus there are many, many more irrational than rational numbers.

Transcendental numbers (from Latin transcedere, "to transgress") are those irrational numbers that cannot be represented as the result of an equation with integral coefficients.†† By contrast, numbers that do satisfy such an equation are called algebraic numbers. The square root of 2, for example, is an algebraic number because it satisfies the equation x² - 2 = 0. The number ►Pi, however, is transcendental, since it cannot be calculated by means of any finite equation.

Decadic numbers are "reversed" irrational numbers. They have infinite many digits before the decimal point but only a finite number of digits after the decimal point. Unlike the real numbers, the plow horses of mathematics, decadic numbers constitute something like a curiosity due to their strange properties. For example, we cannot tell whether a given decadic number is larger than another.††† Thus, the set of decadic numbers is not an ordered set.

Complex numbers are solutions of equations with negative roots. The simplest example is the square root of -1, which is not defined within the range of real numbers. Complex numbers are represented in the form a + b·i, where a and b are two real numbers and i is the square root of -1. Numbers of the form b·i are also called imaginary numbers. Imaginary and complex numbers are frequently used in the natural and engineering sciences — in representing wave functions, for instance.

In addition to these normal numbers there are exotic numbers that are no longer subject to representation by means of numericals:

Transfinite numbers are numbers that are larger than any finite number. The transfinite numbers include ►cardinals (א) and ►ordinals (ω). Transfinite numbers are not part of classical mathematics and are subject to special calculation rules.

Infinitesimal numbers are smaller, that is, closer to zero than any finite number. Just like the transfinite numbers, the infinitesimal numbers are not a part of classical mathematics, though since the 17th century they have been used more often and in more practical contexts in applications of the ►infinitesimal calculus.

Surreal numbers are a special class†††† of numbers that includes everything — real, transfinite, ordinal, and cardinal — as well as infinitesimal numbers. They were defined in 1974 by the mathematician John Conway. On the surreal ►number ray, each real number is surrounded by infinitesimal numbers closer to it than any other real number. Surreal numbers can be used to conduct the wildest mathematical operations such as

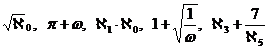
obtaining meaningful results each time.

Hyperreal numbers are similar to surreal numbers and, like the latter, include infinitesimal as well as transfinite numbers. However, they were constructed in the 1960s in a different, more formal manner by Abraham Robinson as the basis of non-standard analysis. Hyperreal numbers can be used to reformulate the ►infinitesimal calculus entirely without limit values.

The various sets of numbers have different kinds of "infinity". Integers can become infinitely large. Rational numbers not only can become infinitely large, but can also be divided infinitely. Real numbers can become infinitely large, can be divided infinitely, and in addition may have infinitely many digits after the decimal point. Finally, the transfinite, infinitesimal, surreal, and hyperreal numbers are not just capable of becoming infinitely large or small as a limit value; they already are these things. For while the other numbers possess only potential infinity, these numbers are actually infinite.

Integers, rational and algebraic numbers are ►countable while real numbers are not. For this the transcendental numbers are to blame. While in reality we know only a handful of transcendental numbers, among them the number ►Pi and Euler's number, they actually constitute the vast majority of all numbers.

To complete this excursus on numbers, here are some examples of small, large, or otherwise remarkable numbers:

0	The number Zero, discovered by Indian mathematicians about 900 BC.
1	From this we can construct all rational numbers: 1+1, 1+1+1, (1+1)/(1+1+1), etc.
1.6180339887...	Golden Cut, an algebraic number.
3.141592654.	The number Pi, a transcendental number.
4	Number of observable dimensions of our world (3 spatial, 1 temporal).
11	Number of real dimensions of our world according to String Theory resp. M Theory (10 spatial, 1 temporal).
42	Answer to the question of life, universe, and the whole rest.
299792458	Speed of light in a vacuum in meters per second.
43252003274489856000	Number of possible configurations of Rubik's Cube.
6670903752021072936960	Number of soluble sudoku puzzles.
6.022045 · 10²³	Number of atoms in twelve grams of carbon.
10²⁷	Number of grains of sand in the Sahara.
10⁶³	Number of grains of sand that it would take to fill the universe (Archimedes's sand number).
6 Phantastilliards	Dagobert Duck's assets.
Googol (10¹⁰⁰)	Largest pronounceable number in the Western hemisphere (origin of the search engine Google's name).
Asamkhyeya (10¹⁴⁰)	Largest pronounceable number of the Eastern hemisphere (from Sanskrit for "uncountable").
2⁶⁵⁵³⁶- 3	Value of the Ackermann function a(4.2).
2^32582657- 1	Largest prime known as of the end of the year 2006.
10 to the power of 10⁸⁰	Average distance to the closest parallel world in any units of length.
Googolplex	10^Googol
10 to the power of 10 to the power of 10³⁴	Skewe's number, the second-to-largest finite number ever used in a mathematical proof (in 1933).
G₆₄	Graham's number, the largest finite number ever used in a mathematical proof (in 1971).
ω	Omega, the smallest number larger than every finite number.
א₀	Aleph-zero, the number of all natural numbers.

* If we printed this number out in a book, the latter would weigh 10⁷⁰ tons, even if it were printed with minuscule letters on extremely thin paper. This would be far heavier than the entire observable part of the ►universe. Since the book would immediately collapse under its own weight, the energy released in this process would trigger a thermonuclear fusion reaction (¹²C+¹²C => ²⁴Mg). As a result, the exterior book cover would heat up to around 600 million degrees Celsius, explode, and thereby create new galaxies. After only a few million years the further contracting book core would fall below the Schwarzschild radius and become a gigantic ►black hole devouring the Milky Way and all nearby galaxies. Thus, the advantages of double powers of ten should not be underestimated.

** Flops is a unit of measurement for the efficacy of microprocessors (Floating Point Operations per Second).

*** Here is the proof. A number with finitely many digits after the decimal point (such as 0.123) is obviously rational, since it can be easily represented as a fraction (123/1000). A number with infinitely many digits after the decimal point such as z = 0.123123123..., also is a fraction, for 999∙z = 1000∙z - z = 123.123123123... - 0.1231231213... = 123, and therefore z = 123/999.

† Here is the proof that 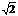is irrational. Suppose that 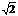could be represented as a fractionn/m. The at least one of the numbers m and n must be odd, or else the fraction could be further reduced. By squaring we obtain 2 = n²/m², and hence n² = 2m². Since 2m² is an even number, n² - and hence also n - must be even as well. For if n were odd then n could be represented as 2k+1; but (2k+1)² is 4k²+2k+1, thus always odd. Consequently, n = 2k and n² = 4k² = 2m², hence 2k² = m²; thus m must be even as well. But this is a contradiction. It follows that 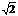cannot be represented as a fraction n/m.

†† An equation of the form a₀ + a₁x + a₂x² + ... +a_nxⁿ = 0, where n is finite and all a are integers.

††† If, for example, we add the two periodic decadic numbers ...444444 and ...555556 in accordance with the standard rules of addition then we obtain 0. Thus, ...555556 is not the least bit larger but instead is the negative value of ...444444.

†††† A class is an ordered set of elements such as numbers together with arithmetic operations such as +, -, ∙, /, that can be applied to these elements.