Dimension: the number of degrees of freedom in a system. The dimension number of a space is based on the number of numerical values that are required to fully determine a position within that space.
A one-dimensional space is a line; here one numerical value suffices to determine a position on the line. A rough illustration of this would be the mileposts on a highway -- although of course an actual highway has more than one dimension. A plane has two dimensions and, accordingly, requires two numerical values to determine a position on it -- for example, longitudes and latitudes on a map. Our familiar everyday space has three dimensions. Airplanes notify their ground stations of their position by communicating three numerical values: their longitude, their latitude, and their altitude.

Spaces with one, two, and three dimensions
Physics frequently deals with more than three dimensions. Special and general ►relativity theory both refer to events and therefore use four dimensions in order to determine the position of such an event -- three for its spatial location and one for the time of its occurrence. Physical systems are frequently described by means of the six-dimensional phase space. In this space three numbers specify the spatial position of an object and three additional numbers specify its momentum, so that altogether six numbers are required to fully determine the state of an object. If we construe this state as a six-dimensional position in an hypothetical phase space, we can conduct calculations in an easier and more elegant way than with merely three dimensions.
According to string theory, our space possesses not just three, but no fewer than ten dimensions, although seven of these are so minutely "rolled up" that we do not notice them in practice. We can imagine a rolled-up dimension for a position on the surface of an extremely long, extremely thin tube or of a hosepipe like this:
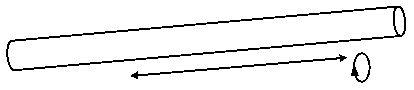
This system actually has two dimensions. To fully specify the position of an object we need to determine where it sits along along the tube (how far it is from each of the tube's ends) as well as its perimeter position, which tells us whether the object sits on top, at the bottom or on one of the sides of the tube. If, however, the tube is extremely thin and we look at it from a great distance, then one numerical value would be sufficient, namely the longitudinal parameter. The reason is that in this case the perimeter value is so small that it is not even "seen" when looking at the object. Thus, the tube practically turns into a line before our eyes. Only when we consider extremely small scales will we need to take the hidden, rolled-up dimension into account.
In 1874, the mathematician ►Georg Cantor asked himself whether the number of points in a space depends on its dimensions. Obviously, the number of points in any given segment or plane is infinite. But does a cube contain more points than a line? Since a plane consists of an infinite number of lines and a cube of an infinite number of planes, we would think that this question should be answered with "Yes" without deserving any further scrutiny. But Cantor always wanted to know everything in full detail. He pondered whether there was any way to precisely correlate positions in a plane with positions on a line. If for each point in the plane there was exactly one point on the line, then both would have to have the same number of points. Now because of its two-dimensionality, we need two numbers to determine a position in a plane. Let us call them x and y, respectively; for example,
x = 1.97538642
y = 2.46801357
Cantor was astonished to discover a simple method by which these two numbers can be correlated with the number of a position z on a line:
z = 12.9476583081634527
He had managed to obtain the new position by alternately applying the digits of the numbers x and y. Thus, if x = x1x2x3x4x5. and y = y1y2y3y4y5., then z = x1y1x2y2x3y3x4y4x5y5. Obviously, this method works for all possible numbers x and y. The only requirement is that these numbers be ►real numbers, that is, numbers with any desired number of positions after the decimal point. A similar method can be used to correlate points in a space of any dimensionality with points on a line. Thus, the number of dimensions in a space is completely irrelevant to the number of points within it.
This was a most astonishing result, which dealt another blow to the already shaken mathematics of the 19th century. "I see it but I don't believe it!", wrote Cantor to his friend, the mathematician Dedekind, right after he found this proof.