Pi (from Greek perifereia, "circumference"): the 16th letter of the Greek alphabet and the circumference of a circle with a radius of 1. Pi is the best known ►real number — that is, the best-known number with an infinite number of non-repetitive digits after the decimal point.
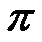
Since antiquity mathematicians have cut their teeth attempting to calculate the mathematical constant π. The first attempt was made in the Bible (Kings I 7.23): "Then he made the molten sea. It was round, ten cubits from brim to brim, and five cubits high, and a line of 30 cubits measured its circumference."
Thus, according to the Bible's directions for the construction of a round bathtub, the value of π is 30/10 = 3.0. For what is supposed to be the infallible word of God, this is not too impressive, especially since around the same time the Egyptians were able to calculate much more precise values. Their approximate value of π was (4/3)4, which comes short of the actual value by less than 1%. ►Archimedes estimated the value of π as 3.14145 by approximation, using a polygon with 192 sides. After that, however, there were no further attempts to determine π until the end of the middle ages.
In 1593 the French mathematician François Viète discovered an esthetically pleasing π calculation formula, which however proved to be difficult to apply in practice: the infinite product
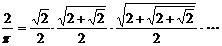
In 1596 Ludolph van Ceulen delivered a calculated π value that was exact up to 35 digits after the decimal point. He had dedicated 30 years of his life to reaching this result. His calculation did not rely on Viète's formula but proceeded in the manner of Archimedes' method by adding the lengths of the sides of a gigantic polygon with 262 sides:
πLudolph = 3.1415926535897932384626433832795029
Ludolph van Ceulen was so proud of this number that he had it engraved on his tombstone. It was long assumed that this achievement was unsurpassable. However, in 1650 the British mathematician ►John Wallis came up with a new formula:
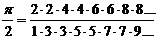
Wallis arrived at this product by a successive approximation to the circular integral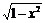 
in the range from 0
to Pi. But even Wallis's formula converges rather slowly, so that many terms must be multiplied to obtain just a few π-digits after the decimal point . The same can be said for the first π-approximation as ►infinite sum published almost simultaneously in 1671 and 1674, respectively, by the Scottish mathematician James Gregory and
the German philosopher/mathematician ►Gottfried
Wilhelm Leibniz:
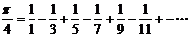
The first useful approximation with a quick convergence rate was discovered in 1736 by the then 19-year-old Swiss mathematician Leonhard Euler:
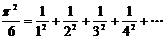
In 1761 Johann Lambert proved that π has infinitely many digits after the decimal point and therefore is an ►irrational number. The transcendence of π was discovered in 1882. Since then we know that it is impossible to determine the exact value of π by means of a finite formula.
Contemporary research on π seeks to identify some patterns or regularities among the digits after its decimal point. To date none have been found. The sequence of digits appears to be entirely random. This also means that any arbitrary sequence of digits must be contained somewhere in the infinite number of digits after the decimal point of π. Thus, Pi contains an encoded version of a complete library of all books that have ever been or will ever be written, including this dictionary and all books on the calculation of π.
At this point the Japanese have adopted the number π. The current record for the number of digits after the decimal point has reached 5 trillion and was established 2010 by Shigeru Kondo and Alexander Yee with a self-made super computer. If you want to participate in the Pi digits record hunt, you can begin with the following lite-C (►www.3dgamestudio.de) program that calculates the first 1000 digits:
int main()
{
video_screen = 0;
wait(1);
printf("\nThe first digits of Pi:\n");
long a=10000, b=0, c=14000, d, e=0, f[16000], g, i=0;
for(; b<c; b++) f[b]=a/5;
for(; c>0; c-=14)
{
d=0;
g=c*2;
for(b=c;b>0;d*=b)
{
d+=f[b]*a;
g--;
f[b]=d%g;
d/=g;
g--;
b--;
if (b == 0) break;
}
printf("%.4d",e+d/a);
e=d%a;
i++;
if (i%19==0) { wait(-0.2); printf("\n"); }
}
printf("\n%i digits printed",i);
}
The world record for memorizing digits of π after the decimal point was set by Akira Haraguchi on July 2, 2005, who memorized a total of 83431 digits. In case you aspire to top this achievement, try memorizing the following numbers — but be aware that to break Haraguchi's record, you'd need to memorize 30 times as many digits as there are here:
3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679
8214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196
4428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273
7245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094
3305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912
9833673362440656643086021394946395224737190702179860943702770539217176293176752384674818467669405132
0005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235
4201995611212902196086403441815981362977477130996051870721134999999837297804995105973173281609631859
5024459455346908302642522308253344685035261931188171010003137838752886587533208381420617177669147303
5982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989
3809525720106548586327886593615338182796823030195203530185296899577362259941389124972177528347913151
5574857242454150695950829533116861727855889075098381754637464939319255060400927701671139009848824012
8583616035637076601047101819429555961989467678374494482553797747268471040475346462080466842590694912
9331367702898915210475216205696602405803815019351125338243003558764024749647326391419927260426992279
6782354781636009341721641219924586315030286182974555706749838505494588586926995690927210797509302955
3211653449872027559602364806654991198818347977535663698074265425278625518184175746728909777727938000
8164706001614524919217321721477235014144197356854816136115735255213347574184946843852332390739414333
4547762416862518983569485562099219222184272550254256887671790494601653466804988627232791786085784383
8279679766814541009538837863609506800642251252051173929848960841284886269456042419652850222106611863
0674427862203919494504712371378696095636437191728746776465757396241389086583264599581339047802759009
9465764078951269468398352595709825822620522489407726719478268482601476990902640136394437455305068203
4962524517493996514314298091906592509372216964615157098583874105978859597729754989301617539284681382
6868386894277415599185592524595395943104997252468084598727364469584865383673622262609912460805124388
4390451244136549762780797715691435997700129616089441694868555848406353422072225828488648158456028506
0168427394522674676788952521385225499546667278239864565961163548862305774564980355936345681743241125
1507606947945109659609402522887971089314566913686722874894056010150330861792868092087476091782493858
9009714909675985261365549781893129784821682998948722658804857564014270477555132379641451523746234364
5428584447952658678210511413547357395231134271661021359695362314429524849371871101457654035902799344
0374200731057853906219838744780847848968332144571386875194350643021845319104848100537061468067491...
Web Links