Uncertainty principle: a physical principle according to which we cannot assign exact simultaneous values to both the position and momentum of an object or physical system.*
In other words, the more exact our determination of the object's position, the more uncertain its measured momentum, and vice versa. This uncertainty principle, which was discovered in 1927 by the physicist Werner Heisenberg, is not due to the fact that measuring an object's position affects its speed and vice versa. Rather, it is an immediate consequence of the wave nature of matter according to quantum theory. The uncertainty principle holds even if, after the object's position is measured, its speed is measured not in the object itself but in an identical copy of it. Similar uncertainty relations obtain between other pairs of physical factors such as energy and time or rotational speed and angle.
An analogy will help to illustrate the uncertainty involved here. Suppose you wish to measure the exact pitch of a note in a musical piece at a precise time. To measure pitch we need to count sound vibrations, that is, maximum excess pressure levels. To do so you'll need to observe the sound wave over a certain period of time.

You count 3 maxima between the dotted lines. The pitch is the number of vibrations n divided by t, that is, in our case 3/t. Since the beginning and the end of the measurement period can be at any given position of the sound wave, the measurement will be uncertain. For if you, for example, shorten or extend t a little, that will not affect the number of vibrations, though you will obtain a slightly higher or lower value for the pitch 3/t. However, the longer the period t, the more vibrations you will count and the more precise your pitch measurement will be. At the same time, the time of your measured sound will become less precise, since the pitch of the musical piece will change during the measurement. The counted value will occur at some point during your measurement period, but you do not know at which point.
In this way, the duration of the measurement period and the pitch behave analogously to the position and momentum of a particle, as the particle possesses a wave nature just like the sound wave.
The uncertainty principle has radical consequences for physics, since it implies that space cannot be infinitely divided. That is because if a particle were fixed to an extremely small spatial region, its momentum, according to the uncertainty principle, would have a correspondingly high degree of uncertainty. In fact, the smaller the size of space into which we "lock" a particle, the greater will be its momentum. Since momentum is energy, and energy is mass, restricting a particle's space can lead to its achieving such an enormous amount of mass that, in the extreme case, it becomes a ►black hole. This sounds like wild speculation, but this kind of increase in mass by spatial restriction really does happen in nature and can be measured. The uncertainty principle is one reason why we cannot apply quantum theory to extremely small spatial and temporal units (see ►Planck units).
*
The formula is as follows: 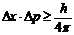 , where Δx is the uncertainty of position, Δp the uncertainty of momentum, and h Planck's constant (see ►natural constants). Having a value of 6,6261 · 10-34 Js, h is very small, so that we cannot observe the uncertainty relation in our everyday world. However, it is clearly noticeable in atomic dimensions.
, where Δx is the uncertainty of position, Δp the uncertainty of momentum, and h Planck's constant (see ►natural constants). Having a value of 6,6261 · 10-34 Js, h is very small, so that we cannot observe the uncertainty relation in our everyday world. However, it is clearly noticeable in atomic dimensions.