Relativity theory: a theory developed by Albert Einstein to describe the large-scale structure of space and time.
Relativity theory actually consists of two theories that complement each other. The development of special relativity theory in 1905 solved the long-standing puzzle of the speed of light, which is independent of both source and recipient. The ►general relativity theory of 1916 described the structure of space and time in the presence of masses causing a curvature in spacetime. To this date, both theories have remained unaltered and have been supported by all relevant experiments and observations. They have revolutionized our view of space and time and been used to describe phenomena such as ►black holes, which escape any attempt at visualization. Since the relativity theories are also important for our understanding of infinity, we here offer a brief introduction.
Special Relativity Theory
Special relativity theory was motivated by the puzzling result of the Michelson-Morley experiments. Toward the end of the 19th century, measurements of the ►speed of light in various directions always yielded the same data no matter how fast the source and the observer moved relative to each other. This contradicts our expectations, for when we try to run at a speed of 10 km/h alongside a fast train moving at 30 km/h, we rightly expect the train to be only 20 km/h faster than us.
This wisdom, however, does not apply to light rays. If we pass at a speed of 100,000 km/s a light ray with a speed of 300,000 km/s, we do not measure a difference of 200,000 km/s. No matter how we hurry along, the light ray will always be 300,000 km/h faster than us. Physicists' attempts to explain this all failed — at least until Einstein, who at the time was a mere clerk at a patent office, turned a vice into a virtue by proposing a bold postulate. He simply declared the ever-constant speed of light to be a property of space itself that does not require any further explanation.
To be sure, this postulate has consequences that contradict our everyday experience, bestowing on Einstein's theory an aura of mystery. The first of these consequences is the phenomenon of time dilation: Moving clocks run more slowly than stationary ones. In fact, in all moving objects time elapses more slowly. Contrary what is commonly supposed, you do not need to be a nuclear physicist to understand this. It is a very easily comprehensible consequence of the ever-constant speed of light.
Einstein's Light Clock
This can be illustrated by the construction of special clock, a so-called light clock. This clock is based on a light ray shooting back and forth between two mirrors.

Whenever the light ray strikes one of the mirrors, the impact is registered by a photo cell, which makes the clock tick forward by another unit. Thus, the motion of the clock is determined solely by the speed of light. Now what happens when the clock moves horizontally?
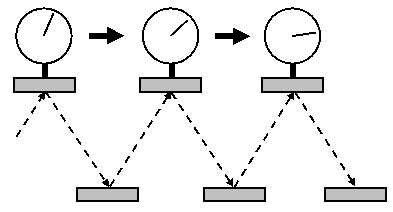
From the point of view of an idle observer, the ray of light now runs diagonally and covers a longer distance than before. Since according to Einstein the speed of light is always the same no matter how the mirrors and the observer move, the ray now requires more time to cover the distance between the mirrors. Therefore, the clock now runs more slowly* — much like a pendulum clock whose pendulum has suddenly become longer.
However, for an observer who moves with the clock, the route of the light ray is the same as before. Accordingly, this observer does not notice that her clock has slowed down. It runs just as fast as all other quartz, atomic, or grandfather clocks that the observer may have with her at the same time. But this means that from the viewpoint of the idle observer, all the moving observer's other clocks and watches must slow down as well; otherwise the clocks would deviate from one another. Hence, the light clock behaves just like any other clock. It is time itself that slows down with the movement of the clock.
The Strange Nature of Motion
Similar considerations can serve to illustrate that not only does time slow down in moving objects but that
 all spatial distances shrink in the direction of movement,**
all spatial distances shrink in the direction of movement,**
 there is no absolute simultaneousness,
there is no absolute simultaneousness,
 the mass of a moving object increases,***
the mass of a moving object increases,***
and
 no material object can be accelerated up to the speed of light.†
no material object can be accelerated up to the speed of light.†
In accordance with this, of course, for the moving observer an idle light clock would slow down, shrink in the direction of its movement, and increase in mass, because from that observer's point of view it moves backwards.
Twins in Outer Space
This theory was hard to swallow in 1905 — not just for the general public but for many physicists as well. That it was nonetheless immediately taken seriously in the scientific world, even though it was proposed by a completely unknown patent office clerk, testifies to the openness of physics. One of the first objections was the twin paradox: One of two twins travels to a distant star while the other remains on Earth. Now, according to Einstein's theory, from the point of view of the twin on Earth, his space-traveling brother ages more slowly, since the latter is subject to time dilation due to the high speed of his spacecraft. Conversely, from the standpoint of the space traveler, his homebody twin on Earth ages more slowly, because from this standpoint the Earth moves backwards at high speed. When the space traveler returns to Earth after many years, which of the twins is the older one?
Some textbooks will tell you that this paradox can only be solved by the (later developed) general relativity theory. But even special relativity theory provides the correct explanation if we accurately compute the data of the twin's space trip. From each of the twins' standpoints, the respective other twin ages more slowly throughout the trip — except for the moment in which the spacecraft slows down and begins its route back to Earth. During that process of deceleration, the twin on Earth suddenly ages at a dramatic speed from the standpoint of the twin in space. Once the twins reunite on Earth, the space traveler will look noticeably younger than his brother — apart from the strains of his trip.††
The twin phenomenon was first confirmed in 1971 with the help of precise atomic clocks on board a charter plane during an intercontinental flight. All other predictions of special relativity theory were tested as well by experiment and observation. To conduct such a test, you don't need to travel into outer space, or even board a fast airplane. Even simple electrons on their orbits around the nuclei of heavy ►atoms come pretty close to the speed of light and are subject to relativistic effects. Without them, gold, for example, would not shimmer in a yellowish but rather in a grey-white color just like silver. †††
If you still haven't had enough of relativity theory, please go on to read about ►general relativity theory.
* For the idle clock each tick requires the time t = d/c, where d = the distance of the mirrors, and c = the speed of light. If the clock moves horizontally at a speed v, then the light ray runs along the diagonal route d' and requires for this the longer period of time t' = d'/c. According to the Pythagorean theorem we have d'2 = d2 + (v∙t')2 = (t∙c)2 + (v∙t')2 and therefore t'2 = t2 + t'2∙(v2/c2). Solving the equation for t' yields
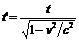
This is the famous formula for time dilation in special relativity theory.
** To illustrate this, consider a light clock that moves upwards, that is, in the direction of the light ray. Corresponding to the time dilation, the contraction of the length will amount to:
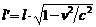
This is the Lorenz contraction, named after the mathematician Hendrik Lorenz, who established this formula even before Einstein.
*** The relativistic mass amounts to:

This is the basis for the well-known Einstein formula E = mc2, in which E is the kinetic energy and m the mass increase of the object.
† This is because upon reaching the speed of light, the object's mass becomes infinite and time stands still, according to the time dilation formula.
†† Numerical example for a trip at 60% of the speed of light to Alpha Centauri at a distance of 4.5 light-years. From the standpoint of the twin on Earth, the trip there and back each requires 4.5/60% = 7.5 years. The time dilation t'/t amounts to 0.8; that is, the space traveler ages on his way there only by 7.5∙0.8 = 6 years. Furthermore, due to length contraction, for him the length of the route contracts to 4.5∙0.8 = 3.6 light-years, so that he indeed needs only 3.6/60% = 6 years for this route. Since for him time on Earth runs more slowly, it will appear to him at his arrival on Alpha Centauri as if only 6∙0.8 = 4.8 years had passed. However, once he is in the process of turning back, all of a sudden 5.4 years will pass on Earth at a frantic speed. Thus, together with the 4.8 years he needs for his way back, from the standpoint of the space traveler a total of 4.8+5.4+4.8 = 15 years will have passed on Earth, while he actually spent only 12 years in outer space.
††† Today there are still vehement opponents of special relativity theory — not among scientists, but among interested laypersons. Some of these critics have indeed understood the theory pretty well but reject it due to the fact that it contradicts our everyday observations. It is worthwhile looking at the arguments of the more serious critics, even if just as a mental exercise, and to figure out where their errors lie. A good source for this is the (German) website "Critique of Special Relativity Theory" listed below.
Links Related to the Topic
■ The Principle of Relativity
■ Critique of Special Relativity Theory
■ Einstein was wrong, the aether exists
■ A Formula Changes the World
■ E=mc2