Distance: the space between two objects.
Cosmic distances play a crucial part in all considerations concerning the beginning and end, as well as the finitude or infinitude, of the ►universe. That is why the subject will receive an unusually long section for this dictionary. In determining the distance between two heavenly bodies, astronomers are typically confronted with two problems: How do we know the distance between us and some point or patch of light in the sky? And what is distance, anyway? If you think that the answer to the second question is trivial, read on.
What is Distance?
Even on Earth, the term "distance" is ambiguous. If we regard the Earth as a two-dimensional surface, distance would simply be the shortest possible route on that surface from one location to another. Thus, this route follows the curvature of the Earth's surface and, as passengers on a plane can confirm, usually appears on a map of the world as a curved line. If, however, we look at the Earth as a globe in three-dimensional space, then the distance between two locations on it will be a straight line cutting right through the globe.
Hence, what we mean by "distance" in a given context depends on the geometry of the space under consideration. Conversely, we use a definition of distance in order to determine the geometry of space.* But the question of distance becomes even more complicated when applied to a space that is expanding, such as our universe. For in this case, the distance between an observer and an object depends on the time of measurement. Due to the finite ►speed of light, we do not see distant objects at their present locations. Rather, we see them at the locations they occupied at the time they emitted the light now reaching us. Thus, when looking at something from a distance we actually look into the past.
Light Rays and Illusionary Giants
►Astronomy differentiates between (at least) four types of distance:
An observed object's proper distance is the distance to its present location — what we most commonly mean by "distance". Proper distance depends on the geometry and expansion rate of the universe. We can think of a theoretical measurement of proper distance as if many scientists lined up along a hypothetical line toward the object and proceeded to determine their distance to their immediate neighbors. The sum of all these partial distances is the proper distance of the object. Distance values that you find in this dictionary are usually for proper distances. The proper distance to the edge of the universe's visible part is 46 gigalight-years.
Light travel distance is the length of the route that the light emitted from the object travels until it reaches us. Since the universe was smaller at the time the light was emitted than today, the object was once closer to us. Hence the light travel distance is also smaller than the proper distance of the object and determines at the same time the age of the ray of light. The light travel distance to the edge of the universe's visible part is only 13.7 gigalight-years — less than a third of its proper distance. This is because the cosmic ►background radiation that reaches us from the edge of the universe emerged shortly after the ►big bang 13.7 billion years ago.
Angular distance is
the "observed" distance of an object. Closer objects tend to appear larger to our eyes and more distant ones, smaller; this is the phenomenon of ►perspective and is used to estimate distances. We can calculate the distance of a visible object (such as a galaxy viewed through a telescope) on the basis of its apparent diameter, using familiar laws of trigonometry. Of course, the distance thus calculated could only be the one pertaining to the time the light we are now seeing was emitted. Thus, the angular distance determines only the distance between the object's position at that time and the position of the Earth at the same time (or else the position at which the Earth would have been if it had existed at the time).
Angular distances are always smaller than the corresponding light travel distances and become even smaller if the objects are very far away. The reason for this paradoxical behavior is that the light reaching us from faraway objects was emitted at a time when the universe was smaller overall. Thus, these objects were actually closer to us at that time and hence appear to us larger, even though they are now further away from us.
Thus, an object at a light travel distance of 13.7 billion years would appear infinitely large to us. For since that object would have emitted its light shortly after the big bang, the universe must have been extremely small at the time it did so. As a result, the object would at the time have been at practically the same location as that occupied by the Earth later on. An example for such an object is the cosmic background radiation already mentioned above, which came into being 13.7 billion years ago and therefore now takes up the entire space of the firmament. But even "normal" heavenly objects such as galaxies and quasars become "illusionary giants" at a proper distance of about 15 gigalight-years or more, appearing larger to us the further they are away.**
In a certain sense, redshift is the mother of all cosmic distances. It is a perceived distance just like angular distance, but unlike the latter, it is based on the object's apparent color rather than its apparent size. Due to the permanent expansion of all spatial structure, the light emitted by any heavenly object expands as well while en route to us. The longer the light takes to reach us, the greater is the expansion. In turn, the light wave's expansion increases its wave length, making the object appear "redder" — an effect that can be precisely measured by means of spectral lines.*** Thus, using redshift is the most important, most precise, and at the same time most simple, method of determining distance.
Redshift was first observed in 1929 by the astronomer Edwin
Hubble at Mount Wilson Observatory in California. Hubble measured the color spectrum of lights emitted by distant galaxies and noticed that their spectral lines were shifted toward the spectrum of closer galaxies. He developed a formula that describes the connection between shift and distance.****
The Redshift Error
Contrary to what is still claimed in many books today, cosmic redshift is not caused by a Doppler effect† resulting from the stars' "drifting apart" from one another. Other alleged causes such as the light's "wearing out" on its long route should be discarded. This is evidenced by the fact that the light is not only shifted into the red spectrum, but really expands. This is why we see cosmic events as if in slow motion. When a supernova lights up, the further it is from us the longer the process seems to take.
There are still other kinds of redshift that have nothing to do with distance. First, the proper distance of stars and galaxies generates minor red- or blueshifts by means of a (this time real) Doppler effect. Our Milky Way, for instance, moves at about 370 km/h relative to the rest of the universe toward a location that is called the ►great attractor. This is why in that direction the stars appear blueshifted, and in the opposite direction they appear redder than they would be just on the basis of the cosmic redshift.
Second, light wavelength is also affected by gravity. Light leaving a gravitational field loses energy and becomes redshifted. This effect is especially strong near the extreme gravitational fields of ►black
holes. At great distances, however, these effects are much less dramatic than those caused by the expansion of space itself.
Thus, if you happen to read in the newspaper that a galaxy twelve gigalight-years away from us has been discovered, you need to ask yourself whether the author means the proper distance, the light travel distance, or the angular distance of that galaxy.†† Due to this ambiguity, astronomers prefer to state only the redshift of very distant objects. With this information, we can easily determine the three other kinds of distance, and with it the age of the object or event corresponding to its light travel distance, by means of the diagram below. In closer objects — those within a vicinity of under 2 gigalight-years — all of these distances are the same, since in that vicinity, the expansion of the universe is negligible.
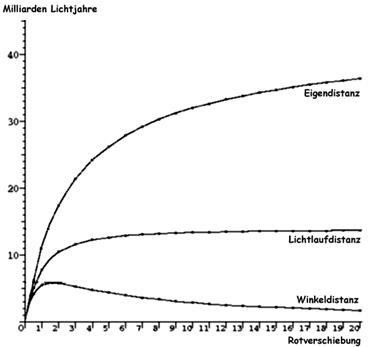
Cosmic Distances and Redshift
Considering the above, one would think that the discovery of redshift had solved once and for all the problem of how to determine cosmic distances. Unfortunately, that is not the case. On one hand, cosmic redshift obtains a measurable value only at a distance of several gigalight-years or more; at lesser distances, the impact of gravity and of the proper motion of the stars is stronger. On the other hand, the exact connection between redshift and each of the other types of distance has yet to be determined. It depends on the speed of the universe's expansion, which in turn changes with time. This makes calculations even more complicated.
For this reason, astronomers try to determine the distance of many objects independently of their redshift, as far as this is possible. The result can then be used to determine the expansion rate of the universe at different times and, through that, the exact connection between redshift and distances. Hence, measurement of distances is one of the crucial areas of astronomy, one that has among other things made possible the discovery of ►dark
energy as the factor responsible for the constant acceleration of the universe's expansion.
30 Ways to Determine Distance
So how do we measure the distance of a tiny spot seen through a telescope as flickering faintly up there on the firmament? Of course, one possibility would be to simply travel there and record our traveled route. But as long as we lack the convenience of interstellar spaceships, we will have to content ourselves with determining distances in some other way. To date, astronomers have devised about thirty methods for this purpose, of which the most important ones are listed below:
Parallax.
This was the first and simplest way to determine distances of nearby stars. It is based on the apparent change in the position of the star corresponding to a (real) change in the position of the observer. If you look at your pointed forefinger alternately with your right and your left eye you will notice that the finger appears to shift relative to its background. You get a similar effect if you observe stars from two different positions on the Earth's orbit.
The shift is minimal compared to the proper motion of stars, which is why it is hard to observe. In 1838, Friedrich Bessel performed the first parallax measurement on the star 61 Cygni. Within a period of 6 months, the star shifted on the firmament by 0.6 archseconds, which corresponds to a distance of approximately 11 light-years.†††
In the 1990s, the satellite HIPPARCOS was used to perform precise parallax measurements for many stars close to the sun. The space probe GAIA is scheduled for the measurement of one million stars in 2011 with even greater precision. GAIA is able to directly determine the distances of all stars in our Milky Way at an accuracy of 10%, even at a distance of 30,000 light-years. Unfortunately, this simple method is not suitable for determining the distance of stars or galaxies millions of light-years away from us, as the parallax angle becomes too small at such distances. But don't worry: Astronomy's bag of tricks contains many more methods of distance measurement.
Stellar parallax.
In star clusters such as the Pleiades or the Hyades, which move as one unit, distance can be determined by observing the stars' apparent direction of movement. While in reality the stars move parallel to one another, due to perspective they appear to us as moving toward or away from a vanishing point on the firmament. If we know the proper motion of the star cluster, we can determine its distance based on the position of the vanishing point.
Velocity of the circulation of stars. Stars orbit around the centers of their galaxies. Thus, we can determine a star's distance from the center of its galaxy in terms of its circulation speed. We can then calculate the distance of a star in the Milky Way with known velocity on the basis of its distance from the center of the galaxy.
Expansion parallax.
In an exploding star, a so-called supernova, the (apparent) magnified telescope image of the explosion cloud can be compared with the (real) velocity of the explosion cloud, which in turn is determined by means of a blue- or redshift of its spectral lines. From both values we obtain the distance of the supernova.
Spectral brightness.
The surface brightness of a star depends on its temperature and
thus on its color: cooler stars are brighter in the red region of their color spectrum, hotter ones in the blue region. If we know the size of a star, we can determine its luminosity based on its color. Subsequently, we can compare its real with its observed luminosity in a telescope, for the further away a star is the darker it appears to us.††††. The only problem is this: How do we know the actual size of the star?
In many special cases we can determine the size by means of methods such as the following:
Baade Wesselink method.
With this method, we observe stars that are subject to changes and whose radius, brightness, and color oscillates between two values. We can then calculate the brightness, and hence the distance, of the star on the basis of the two extreme values of its observed luminosity.
Binary star spectroscopy.
You can determine the masses — and hence the sizes — of two stars circling around one another on the basis of their orbits, which can be observed as regular changes in brightness. The distance of the binary star system can be subsequently determined based on its spectral brightness.
Hertzsprung-Russell diagram.
In the early 20th century, the astronomers Einar Hertzsprung and Henry Russell discovered that there is often a close connection between a star's fluorescent color and its size. This connection can be represented in a diagram. The stars in this diagram are called the main sequence stars. Their distance can be determined directly based on their fluorescent color and observed luminosity.
Cepheid period.
Cepheids are extremely bright giant stars pulsating in a steady pattern due to periodic heating of their surrounding gas shell. The larger a cepheid the slower is its pulsating rhythm. Thus, by measuring the pulsation of the cepheid, we can determine its size and hence, on the basis of its luminosity, also its distance. In this way, cepheids act like yardsticks in outer space that can be used to estimate the the distances of their neighboring stars as well.
Type Ia supernovas.
These are explosions of white dwarf stars in binary star systems. Such a star constantly attracts matter from its orbiting partner; once a certain amount of matter has been accumulated, the star explodes. Its luminosity can be determined quite precisely based on the duration of the explosion.
This is why observed luminosity is a good indicator of distance. Because we can see supernovas even at extreme distances, the distances of explosions provide important information for determining the geometry and expansion speed of the universe.
Tully-Fisher relation.
This relation tells us the connection between the rotational speed of a spiral axis and its total luminosity, for in larger, and therefore brighter, galaxies the external areas rotate faster than the ones closer to the center. Once the rotational speed has been identified by means of the redshift and the observed luminosity of a galaxy, we can also estimate its distance.
Gravitational lens time delays.
►General Relativity Theory tells us that masses, including galaxies, effect a curvature in their surrounding space, thereby acting like lenses that divert light. For this reason, we sometimes see several images of a far-off ►quasar. One of the images reaches us directly, while another may reach us by detour, because its light was diverted by a galaxy. We can then determine the distance of the quasar based on the time delay between the direct and the diverted image, which in turn we can find out by studying changes in the luminosity of the quasar.
The quasar furthest away from us reaches a redshift value of 6.43.‡ At this point it is already at a distance of 30 gigalight-years from us; its emitted light requires 12.8 billion years to reach us. However, there is yet another object in outer space that is even more redshifted: the cosmic ►background radiation mentioned above. It has a redshift value of 1089; thus, its wavelength has expanded more than a thousand times its original value. Its light ceased to be visible long ago, but can still be measured by means of microwave receivers. From the factor 1089 we can calculate the time at which this radiation emerged — namely, 13.7 billion years ago, shortly after the ►big bang.
The Redshift Puzzle
To conclude our excursion on distance, we want to present you with a little (but not at all trivial) puzzle: The energy of a light particle depends on its wavelength. The redder the light the weaker is its energy. Thus, due to cosmic redshift, the energy of the light particles traversing space constantly decreases. At the same time, however, a fundamental law of physics — the Principle of the Conservation of Energy — tells us that energy does not disappear; it can only be converted from one form into another. So where does the energy of light go?‡‡
* Geometry in this context simply means the study of distances. Distances in a three-dimensional Euclidian space (see Parallels) are determined by Pythagoras's law:
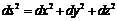
Here, ds is the so-called line element: the distance between two adjoining points whose coordinates differ by the amounts dx, dy, dz. By contrast, the distance between two locations on the surface of the Earth differing in their longitudes φ and latitudes θ is calculated as follows (here, r is the Earth's radius):
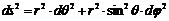
The line element takes on a different value for two locations on the surface of the sphere than it does for the same locations in three-dimensional Euclidian space. A definition of distance in terms of the line element is also called a metric of the respective space. The space-time continuum of our real universe has four ►dimensions - x, y, z and the time t of a given event. Thus, the four-dimensional line element takes on the following value (in a Euclidian space):
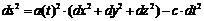
This is the metric of our universe, the so-called Robertson-Walker metric as it pertains to Euclidian spaces. It contains c, representing the speed of light, as well as the scale factor a(t), which determines the size of the expanding space relative to time t.
** The illusionary giant in Michael Ende's novel Jim Knopf has the same reverse perspective as far distant galaxies.
*** Spectral lines are certain wave lengths that radiate heated elements such as hydrogen or helium. If you decompose the light of stars into a spectrum of individual wave lengths, the spectral lines will appear as bright lines in the spectrum.
**** The redshift z is determined based on the ratio between the received and the originally emitted wavelength. This corresponds to the ratio of the size R of the universe to the present time and to the time of emission:
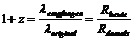
Based on an observed redshift z we can determine the distance of the object by integrating over the velocity of spatial expansion. Though the formula looks somewhat scary, it does take into account the accelerated expansion of the universe due to dark energy:
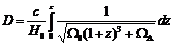
where D = proper distance, c = speed of light (c. 300,000 km/s), H0 = Hubble constant (c. 22 km/s per light-year), Ω0 = percentage of normal and dark matter in the universe (c. 0.27) and ΩΛ = cosmological constant, i.e., the percentage of dark energy in the universe (c. 0.73). In a flat Euclidian universe we have Ω0 + ΩΛ = 1.
The value of the integral can be numerically determined for any given z values by means of a math software program such as Maple or, less expensively, by means of an online calculator such as the one accessible at wims.unice.fr. If you don't feel like doing a complicated calculation, you can read the value off of the distance diagram. The radius of the ►Hubble volumes is thus determined on the basis of the background radiation shifted by z = 1089 to D = 46 gigalight-years.
† Light emitted by objects moving toward us appears to us bluer, while light emitted by objects moving away from us appears redder. The same phenomenon makes the horn of a car speeding toward us sound louder than that of a car moving away from us.
†† Usually the light travel distance, although the proper distance would make more sense.
†††1 archsecond = 1/3600 angular degrees. From the reciprocal of the half shift in archseconds, we obtain the distance in parsec (see ►Astronomy): 1/(0.5∙0.6") = 3.33 Parsec = 10.8 light-years.
†††† The luminosity is proportional to the visible star disk, that is, to the square of the star radius. The observed luminosity is conversely proportional to the square of the distance, that is, a quarter of the emitted light reaches us from twice the distance.
‡ Recently, an object was discovered at an even greater distance, namely, the galaxy ►Abell 1835 IR1916 with a redshift of 10 and a light travel distance of 13.2 gigalight-years. This discovery was possible due to the fact that the galaxy cluster Abell 2218 acted as a ►gravitational lens, magnifying the image of galaxies located behind it.
‡‡ Nowhere. You would think that the energy is used up to provide the required "pressure" for spatial expansion, but in fact the expansion diminishes the amount of spatial energy. Strictly speaking, the Principle of the Conservation of Energy is valid only for so-called inertial systems, that is, systems that are not subject to possible acceleration. Due to its expansion, the universe is not an inertial system. The total energy decreases in an expanding universe, while it increases in a collapsing universe.
Links Related to the Topic
■ Redshift
(Wikipedia)
■ Astronomical Distance Measurement (OpenDirectoryProject)