Dedekind cut: a method of deriving the ►real numbers from the rational numbers.
The mathematician Richard Dedekind designed this method of number derivation toward the end of the 19th century. Suppose you wish to construct the square root of 2, which is not a rational number (that is, it cannot be expressed by means of a fraction*). To be sure, we can find a sequence of fractions the value of whose square increasingly approaches the number 2. Thus,** we can find an infinitely ascending sequence of fractions whose squares are all smaller than 2 but -- if we just follow the sequence far enough -- differ from 2 by less than any previously specified amount. Suppose that we stipulate a diminutive amount such as a trillionth. Beginning with a certain element in our sequence, all subsequent elements will have squares that differ from the number 2 by less than one trillionth. In the same manner, we can construct an infinitely descending sequence of fractions whose squares are always larger than 2 but from some point onward differ from 2 only by an amount less than any previously specified amount.
In this way we have seemingly surrounded the square root of 2 from both the top and the bottom. Thus, it is hardly conceivable that it will continue to slip through our fingers. But it remains a fact that we will never quite reach the square root of 2 in this way.
The square of each fraction will always be either larger or smaller than 2. Let us now divide up all fractions into two sets according to whether their squares are or are not smaller than 2. We will see that the fractions whose squares are smaller than 2 do not have a maximum limit, and that the fractions whose squares are not smaller than 2 do not have a minimum limit. The difference between the fractions whose square is not smaller and those whose square is smaller than 2 does not have a bottom limit except zero. In between the two sets -- where we would expect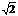 
to be
-- is nothing. Though we placed the termini of our two sequences as close as possible to one another, we have not succeeded in capturing the square root of 2.
Now the above method of dividing up all elements of a sequence into two sets such that one comes entirely before the other in the total sequence is called a Dedekind cut. As applied to the rational numbers, such a cut constitutes a complete definition of the real number located inside the "gap" but does not contain it.
* Proof: Suppose we could represen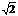t as a fraction of the form n/m. Then at least one of the numbers m or n must be odd, or else the fraction could be canceled further down. The square of the fraction will then be 2 = n2/m2 and hence we have n2 =
2m2. Since 2m2 is an even number, n2 and n must be even as well. For if n were odd then we could
represent n as 2k+1; however, (2k+1)2 is
4k2+2k+1 and therefore always odd. Hence n =
2k and n2 =
4k2 = 2m2, thus we have 2k2 = m2,
and therefore m must be even as well. This is a contradiction. It follows that 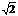cannot be represented as a fraction n/m.
** This exposition is an abridged version from Bertrand Russel's Introduction to Mathematical Philosophy (1919).