Banach-Tarski paradox: the doubling of the volume of a sphere by partitioning it into a finite number of infinitely complex pieces.
A solid ball can be partitioned in such a way that its parts may be reassembled into two solid balls, each of which has the same size as the original. To achieve this, you just need to run through a finite reassembly process by rotating and moving the ball pieces around (without changing their shapes). This is probably one of the most astonishing theorems of contemporary mathematics. It was first proven in 1924 by the Polish mathematicians Stefan Banach and Alfred Tarski.
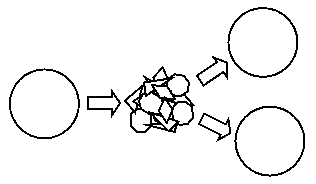
The paradox relies upon the representation of a volume by an infinite number of points. You may even partition the ball into a finite number of pieces, as long as the pieces are sufficiently complex -- like a sponge with an infinite number of pores, for example, or an infinitely fine-grained dust cloud. The proof (available to interested readers under "Links Related to the Topic", below) is applicable to spaces of indefinite ►dimensionality, though not to two-dimensional planes. Furthermore, it is applicable to bodies of any shapes -- including, for example, the shape of a gold bar. And since the operation of partitioning and reassembly may be applied an indefinite number of times, we are accordingly able to obtain an indefinite number of copies of the original body. Unfortunately, real physical objects consist not of an infinite number of points, but rather of a finite number of ►atoms. That is probably why no one has ever succeeded in partitioning and multiplying real gold bars in this way.
Links Related to the Topic