Countability | dictionary.of-the-infinite.com

Countability is a property of sets*: the property of having just as many elements as the totality of ►natural numbers or of some subset thereof.

That a set is countable means that its elements can be counted, at least in principle. Obviously, finite sets are always countable. The set of all grains of sand in the Sahara is large -- probably too large for the counting of them to be a practical possibility. (That's not to mention that some grains would get blown away after being counted and you'd have to keep starting over!) Nevertheless, in principle they could be counted -- and as a matter of fact, there are about 1,224,000,000,000,000,000,000,000,000 grains of sand in the Sahara. But what about sets with an infinite number of elements?

The most simple example is the set of all natural numbers: 1, 2, 3, 4, ... This set is of infinite cardinality since there are infinitely many natural numbers**. But at the same time, the set is countable since it is the very set that defines countability, as we saw above. Are there any other countably infinite sets? Could it be that every infinite set is countable? In the 19th century, the mathematician ►Georg Cantor was the first to deal with these questions; he discovered astonishing and at first paradoxical-seeming properties of infinity. He was also the one who first defined countable infinity as a property of certain infinite sets.

To understand the concept of countable infinity, let us first try to obtain a more concrete notion of counting in general. For counting an infinite number of items is hard to imagine, especially since it would take an infinite amount of time. So what does it actually mean to count things in general?

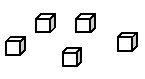
How do we know that these are five cubes? If in counting them you successively point to the individual cube one by one while murmuring to yourself, "One, two, three, four, five," then your procedure is mathematically correct. In counting, we associate consecutive natural numbers with the items counted. The total number of items counted corresponds to the natural number assigned to the last item -- in our case, the number five. Thus, we can count the elements of a set if we can assign to them consecutive natural numbers, however different the counted items may otherwise be.

If we can enumerate an infinite set of items in this way then we have proven that it is countable. To do so it is not necessary to actually assign each element a number, for this would be an infinite process. Rather, it suffices to prove that doing so is theoretically possible. Once we have proven this, we have thereby automatically assigned each element in our set exactly one natural number; conversely, we have also assigned each natural number exactly one element in our set. It follows that our set has just as many elements as there are natural numbers.

Equipped with this knowledge, we can now go about examining other infinite sets with regard to their countability. Is, for example, the set of all even numbers -- that is, 2, 4, 6, 8 ... -- countable or uncountable? Obviously, this set is infinite as there is no greatest even number. But does it have the same number of elements as the set of natural numbers? There are arguments contra and arguments pro:

Contra: There are only half as many even numbers as there are natural numbers. Therefore, the set of even numbers can have only half as many elements as the set of natural numbers; thus it is not countably infinite.

Pro: Each natural number, no matter how great it is, can be assigned exactly one even number -- namely, its double. Conversely, we can assign each even number exactly one natural number -- namely, its half. Hence, there are just as many even as natural numbers.

Though the "pro" reasoning cannot be refuted, it does appear counterintuitive. The even numbers seem to us "less" than the natural ones, because many natural numbers (and even an infinite number of them!) are not among the even ones. This shows that our intuitive assumption that a totality (such as the totality of natural numbers) is always larger than one of its subsets (such as that of the even numbers) is not applicable in the field of infinity. Even relatively small subsets such as the set of all numbers beginning with the digit 7, the set of all square numbers, and the set of all multidigit numbers with all digits identical contain just as many numbers as the set of natural numbers.

This is one of the paradoxes of infinity. In general, any given infinite subset of the set of natural numbers is countable, that is, equinumerous to the total set of natural numbers. The 19th century German mathematician Richard Dedekind used this notion to provide a general definition of the very concept of an infinite set: A set is Dedekind-infinite if and only if it is equinumerous to one of its subsets. Modern set theory since Zermelo and Fraenkel defines the infinite set as a set that is not finite, and the finite set as a set that is either empty or can be placed in a one-to-one correspondence with a set of natural numbers that has fewer elements than some particular natural number. Only with the help of the axiom of choice, or at least a weak form of it, can it be shown that all Dedekind-infinite sets are also infinite in the sense of Zermelo and Fraenkel, and vice versa.

Now, there are also sets that seem not smaller but larger than the set of natural numbers, such as the set of fractions or rational numbers. Is this set countable?

Contra: Of course not. After all, there are far more fractions than natural numbers. Between any two natural numbers such as 1 and 2 there are infinitely many fractions: 3/2, 4/3, 5/4, 6/5, 7/6, ... Even between any two fractions there are infinitely many other fractions.

Though this is not a proof, it's certainly an impressive argument. Even our countability pope ►Georg Cantor regarded the set of fractions for some time as uncountable while he was looking for a proof. When he finally found one, it turned out to have a completely different result from the one he expected. To examine their countability, Cantor arranged all fractions consecutively in a table extending infinitely to the right and bottom:

1/1

2/1

3/1

4/1

5/1

6/1

7/1

8/1 .

1/2

2/2

3/2

4/2

5/2

6/2

7/2

8/2 .

1/3

2/3

3/3

4/3

5/3

6/3

7/3

8/3 .

1/4

2/4

3/4

4/4

5/4

6/4

7/4

8/4 .

1/5

2/5

3/5

4/5

5/5

6/5

7/5

8/5 .

1/6

2/6

3/6

4/6

5/6

6/6

7/6

8/6 .

1/7

2/7

3/7

4/7

5/7

6/7

7/7

8/7 .

1/8

2/8

3/8

4/8

5/8

6/8

7/8

8/8 .

1/9

2/9

3/9

4/9

5/9

6/9

7/9

8/9 .

. .

Extended infinitely, this table obviously encompasses all existing fractions, as denominator and numerator can each accept any numerical value. Now Cantor created a diagonal sequence of numbers as indicated above by the arrows. The sequence begins with the fraction 1/1 and continues along the direction of the arrow. Cancellable fractions are canceled and skipped if their value has already been listed earlier in the sequence. Thus we obtain the following list of numbers:

Number sequences, however, are always countable. By serially numbering the list positions, each fraction can be assigned exactly one natural number, and vice versa. This proves that the fractions form a countable set. Even though there are infinitely many fractions between any two natural numbers, there are nonetheless just as many fractions as there are natural numbers. This is just another example of how our intuitions lead us astray when we think about infinity.

Is, then, every infinite set countable? Cantor next looked at a set that appears to be even larger than that of the fractions -- namely, the set of real numbers. These are decimal numbers having an indefinite, and possibly an infinite, number of digits after the decimal point -- numbers such as ►Pi, the mathematical constant that expresses the ratio of the curcumference of a circle to its diameter (3.14159.). Fractions (or rational numbers), by contrast, have a decimal expansion that stops (like 1/4 = 0.25) or is periodic (like 1/3 = 0.333... or 1/7 = 0.142857142857142857...)***.

Having become more cautious since his discovery of the countability of fractions, Cantor at first assumed that the real numbers could be enumerated as well in some hitherto unknown way. If this were correct then one should be able to arrange them in a numerical list like the fractions. Let us look at such a candidate list (for simplicity, we shall focus here only on the numbers between 0 and 1):

The order of the numbers does not matter. However, in order to satisfy the requirement of countability for this realm of numbers, the above list needs to include all real numbers between 0 and 1. Cantor now considered a random number derivable from the diagonal in the list. He constructed this number by making the first number on the diagonal be its first digit, the second number on the diagonal its second digit and so on (as underlined above). In this way, he arrived at the number:

He then altered each single digit after the decimal point by adding to each the numerical value 1:

Now, this number obviously another real number between 0 and 1, but it is not contained in the above list! For it is distinguished from each of the other numbers on the list at least by the value of the digit after the decimal point that had been adopted from that number; for in each case, that value has been changed by adding 1. Obviously, this result is valid for all lists of real numbers, no matter in what order the numbers are arranged. Therefore, no conceivable list of numbers can ever include all real numbers between 0 and 1. Still less could the set of all real numbers be represented in any list.

In this way, Cantor proved that the real numbers are not denumerable and thus not countable. In them we appear to encounter a "higher level of infinity" than that of the natural or rational numbers. The various levels of infinity play an important part in the theory of ►cardinals.

* A set is a collection of elements such as numbers. An infinite set is a collection of an infinite number of elements. Natural numbers are positive integers without decimal expansion.

** If it were finite then it would contain a greatest number x. However, x+1 is also a natural number and at the same time greater than x. Therefore, the set of all natural numbers cannot be finite.

*** This becomes obvious from the following consideration. A number with finite decimal expansion (like 0.123) clearly is always a fraction (123/1000). Now let us consider a number n that is periodical, i.e., has an infinite repetition of periods after the decimal point such as n = 0.123123123... Then 999∙n = 1000∙n - n = 123.123123123... - 0.1231231213... = 123 and therefore n = 123/999. This shows that every number with finite decimal expansion or infinite repetitions of periods after the decimal point is a fraction, that is, a rational number.